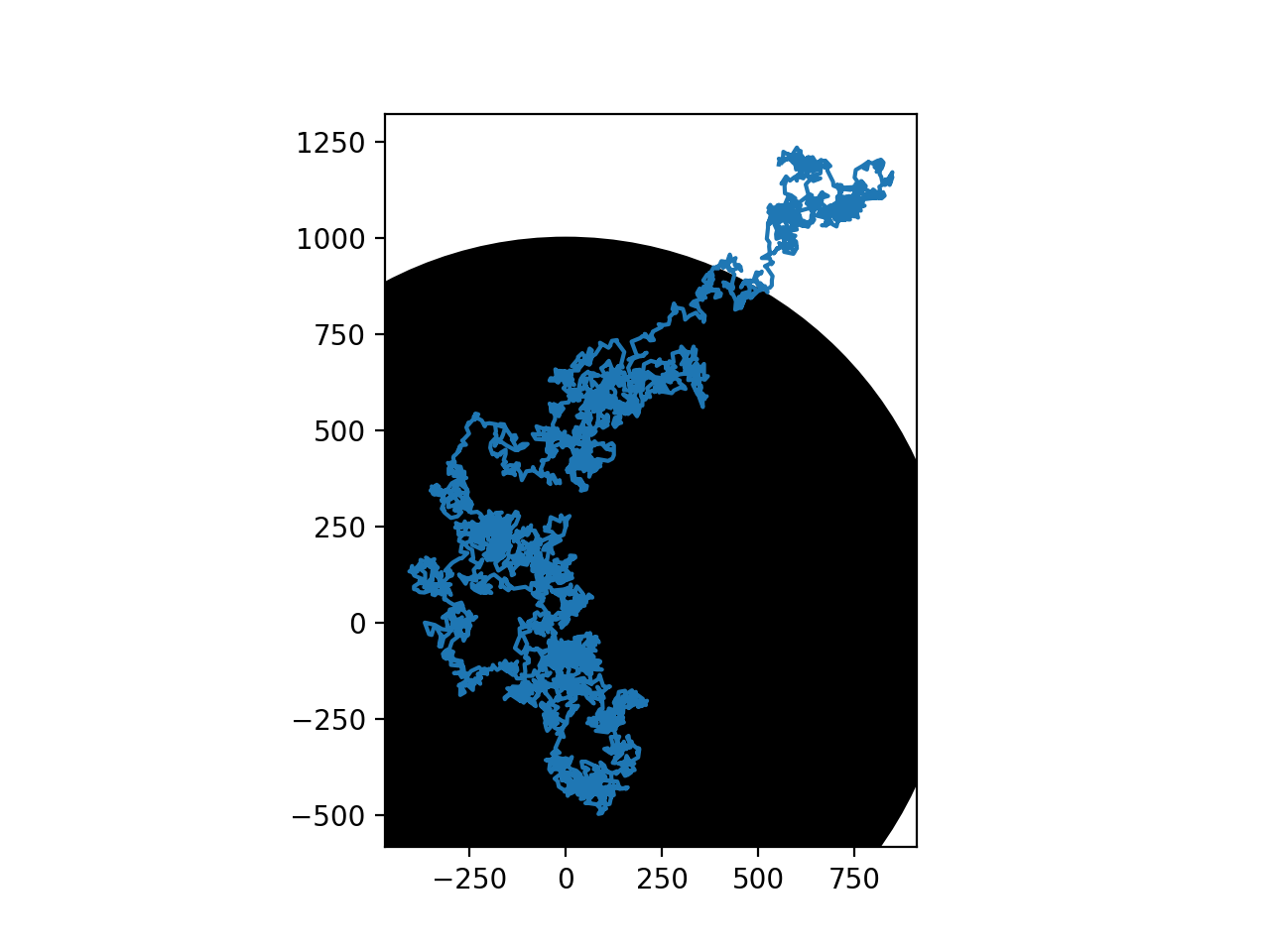
Random walk

Last ned filen uke_13_oppgave_8.py. Du skal tilpasse filen for å løse de følgende oppgavene.

Filen simulerer en «Random walk» (tilfeldig tur) i to dimensjoner. Vi begynner på (0,0) og tar 100 tilfeldige skritt opp, ned, til venstre eller til høyre. Turen er lagret i numpy array steps. Du trenger ikke å endre den delen der vi genererer steps:


###################################
#     generate one random walk    #
###################################
# a list of 4 directions 0,1,2,3
dirs = np.random.randint(0, 4, N_steps)
# a 2D list of steps, empty for now
steps = np.empty((N_steps, 2))
# fill the list of steps according to direction
steps[dirs == 0] = [0, 1]  # 0 - right
steps[dirs == 1] = [0, -1]  # 1 - left
steps[dirs == 2] = [1, 0]  # 2 - up
steps[dirs == 3] = [-1, 0]  # 3 - down
###################################
# use cumsum to sum up the individual steps to get current position
steps = steps.cumsum(axis=0)
###################################

Hver linje i steps inneholder den nåværende x- og y-posisjon, slik at vi enkelt kan plotte turen:

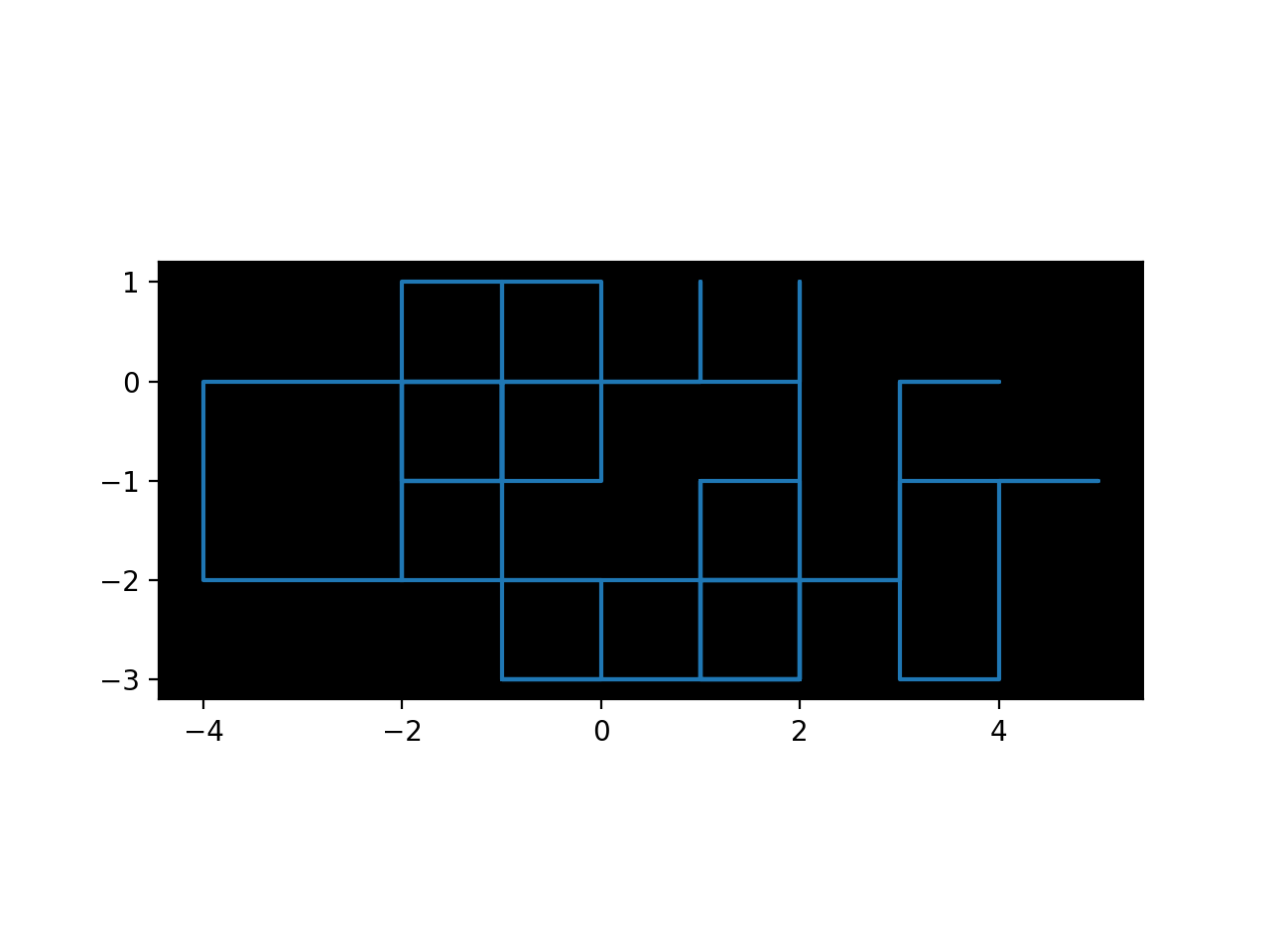
../../_images/walk_100.png

Oppgaver

Send inn den endelige koden som fullfører alle deler som uke_13_oppgave_8.py

(a) Tegn 1000000 (én million) skritt i steden for 100.

../../_images/uke_13_walk_1M.png
(b) Lag ein ny int-variabel

repeats som angir hvor mange ganger vi skal simulere hele turen. Skriv en for-løkke som repeterer simulasjonen frem til plt.plot() repeats ganger. Eksempel for repeats=5, med 1M skritt.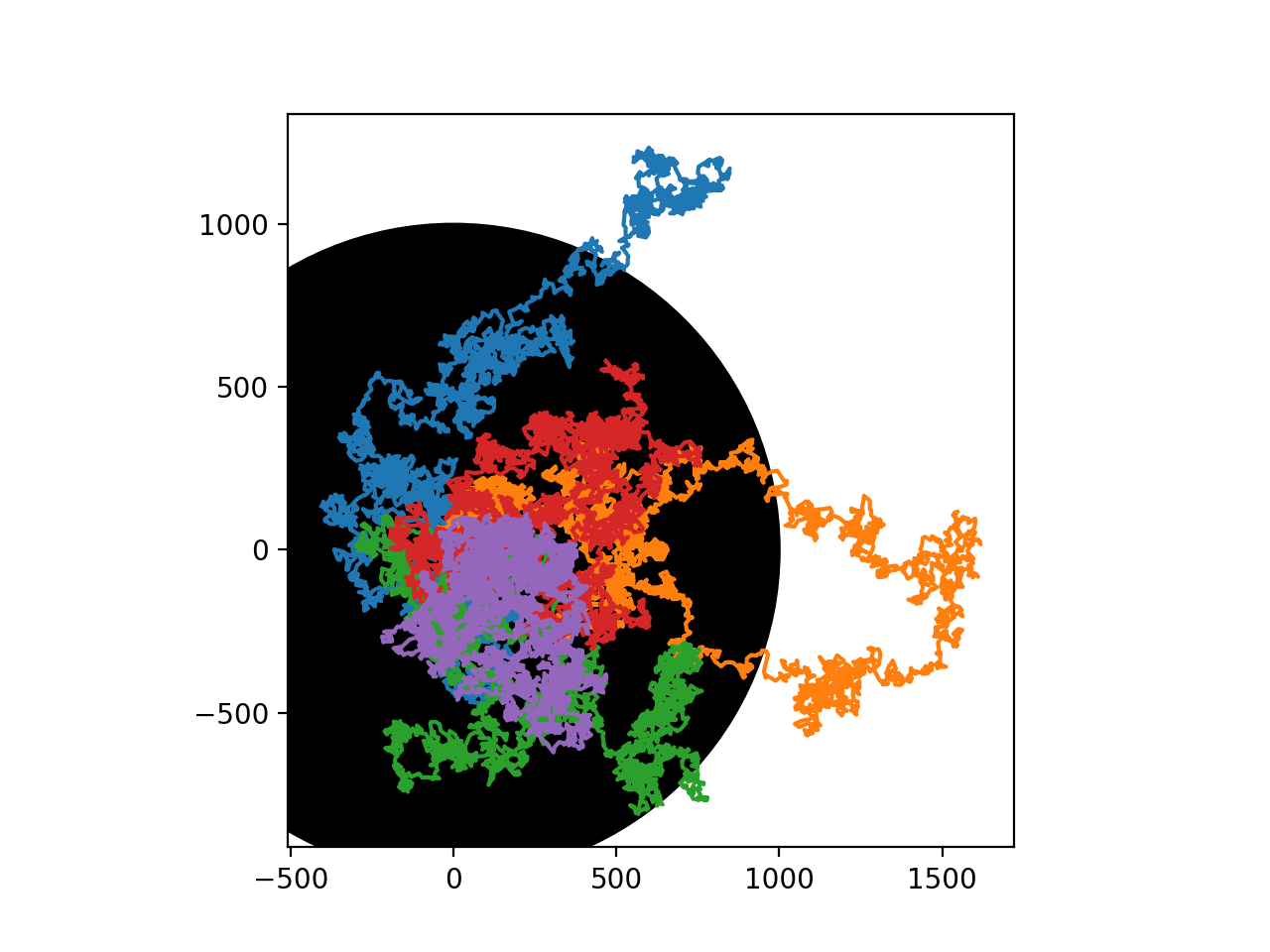

../../_images/uke_13_walk_5rep.png

  1. Legg inn plot-overskriften og endre aksene slik at (0,0) er i midten og alle turer er helt synlig. Overskriften og akse-grensene skal tilpasses når vi endrer N_steps og/eller repeats.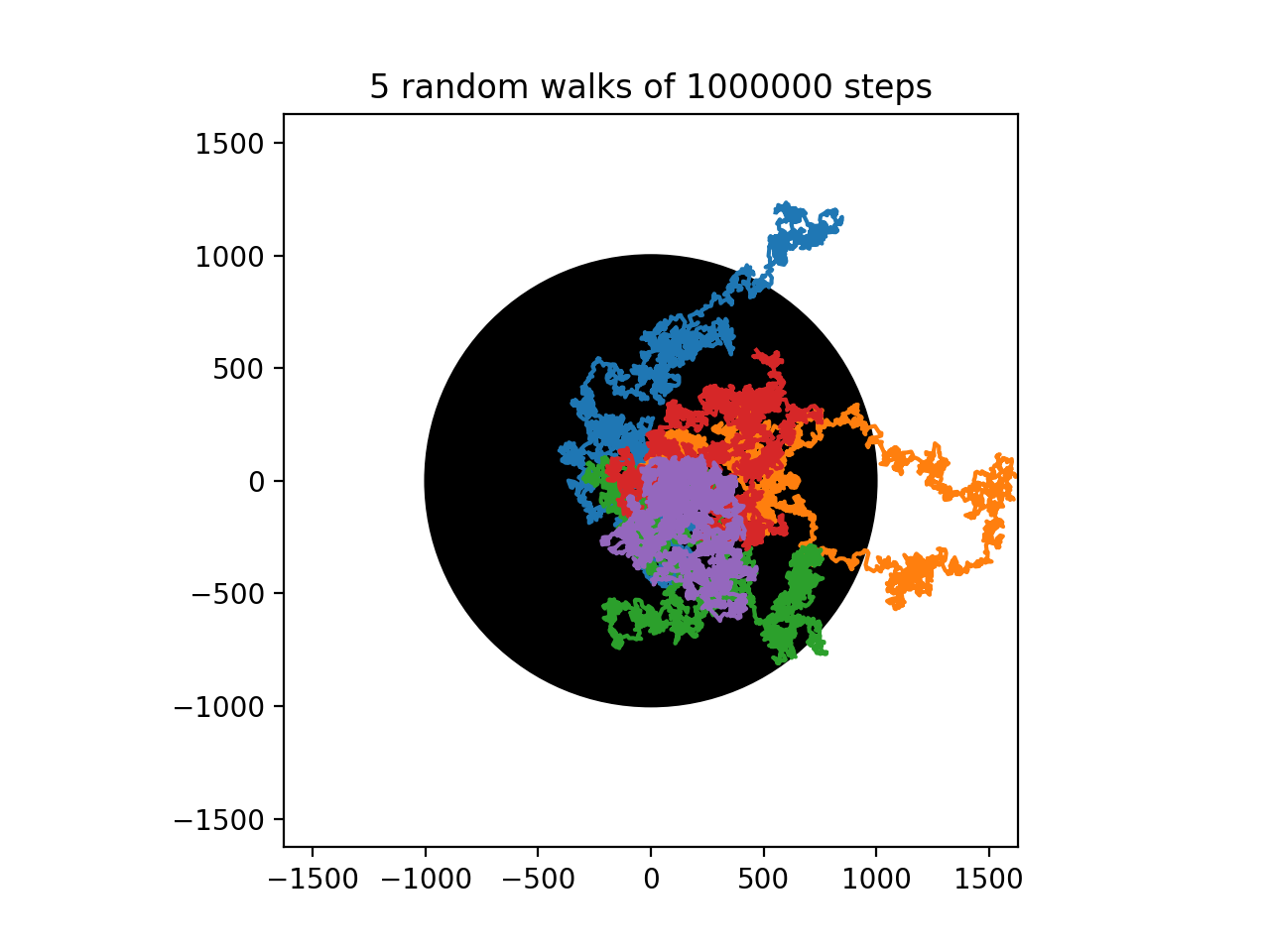

    ../../_images/walk_title.png ../../_images/uke_13_walk_7rep.png

  2. For hver tur, finn maksimal avstand fra sentrum (0,0). Avstand blir regnet ut som \(d=\sqrt{x^2+y^2}\)

    Tips: du kan jobbe med hele numpy-arrayene xs og ys for å få avstandene ds, og så ta maksimum, uten løkke. Lagre resulterende plott for repeats=5 som uke_13_oppg_10.png

    Legg inn maksimal avstand i en «legend»:

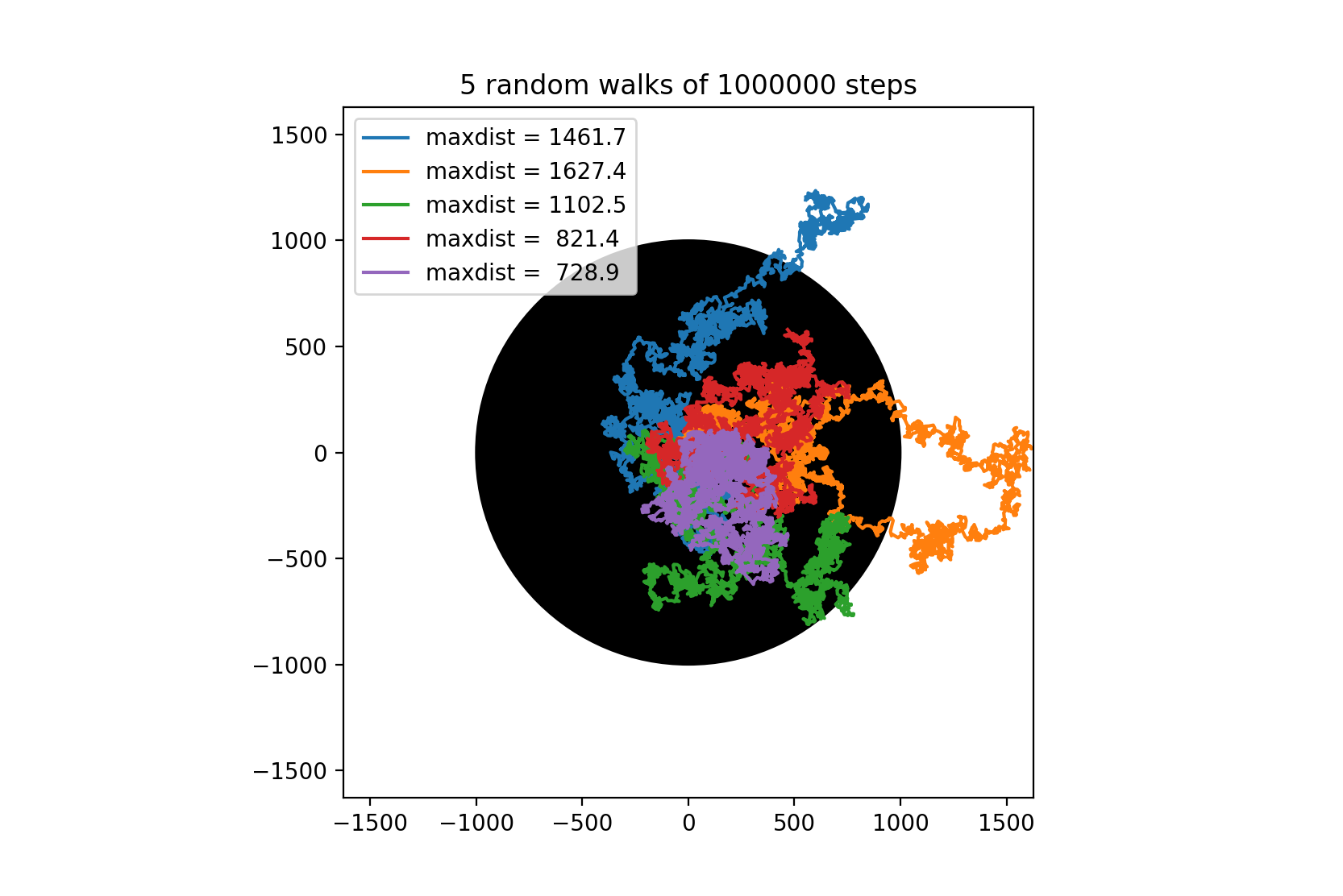
    ../../_images/uke_13_walk_legend.png

    (Tallene i bildet kan avvike. Det kommer an på om du bruker xs og ys før eller etter du har tatt ut skip stegene.)