Uke 11 - modules / import / standardbibliotek¶
Eksempler¶
I Python kan vi dele opp kode i flere ulike filer. Dette blir raskt nødvendig når man gjør større prosjekt. Filene kalles moduler og man kan importere kode i en modul fra en annen modul. Dette skal vi se på denne uken.
Eksempel 1¶
Vi kan gjenbruke funksjoner og variabler fra en annen fil med import. Her er
en fil med noe nyttig innhold (du kan laste ned filen her:
eks_1_lib.py). Sånne filer kalles modul/bibliotek:
# Vi kan definere funksjoner...
def fib(n):
"""Return the fibonacci sequence up to n as a list"""
a, b = 0, 1
seq = []
while a < n:
seq.append(a)
a, b = b, a+b
return seq
def collatz(n):
"""Return the collatz sequence from n as a list"""
def collatz_step(n):
if n % 2 == 0:
return n//2
else:
return 3*n + 1
seq = [n]
while n > 1:
n = collatz_step(n)
seq.append(n)
return seq
# ...eller verdier i en bibliotek
# speed of light [m/s]
C_LIGHT = 299792458
# Planck constant [Js]
H_PLANCK = 6.62607015e-34
I hovedprogrammet kan vi gjenbruke filen på ulike måter: Vi kan import-e hele
filen med sitt navn, eller vi kan gi et nytt navn med import .. as. Se hvordan
vi bruker funksjoner fra filen.
En annen mulighet er å plukke ut spesifikke funksjoner med from .. import ....
Vi kan også bruke as her. (du kan laste ned hovedprogrammet her:
eksempel_1.py)
print('Option 1')
import eks_1_lib #import module
fib_1 = eks_1_lib.fib(100)
col_1 = eks_1_lib.collatz(17)
print(fib_1)
print(col_1)
#################################
print('Option 2')
import eks_1_lib as el
print(el.collatz(5))
c = el.C_LIGHT
print(c,'m/s')
#############################
print('Option 3')
from eks_1_lib import fib
fib_2 = fib(75)
print(fib_2)
##############################
print('Option 4')
from eks_1_lib import H_PLANCK as h, C_LIGHT as c, fib
print(c)
print(h)
print(fib(30))
Advarsel
Pass på at begge filene ligger i samme mappen, og at terminalen kjører derfra.
Ved bruk av import kan man strukturere store programmer på en oversiktlig måte, gjerne også i flere mapper. Det går utover pensum her, men mer informasjon finnes på https://docs.python.org/3/tutorial/modules.html
Obs
Noen ganger kan du se noe slikt som from module import * i Python kode.
Dette importerer alle tingene fra modulen module med sine egne navn. Dette
er ikke en rekommendert måte å importere. Om man importerer fra flere ulike
moduler/bibliotek er det vanskelig å si hvor det man bruker i koden er definert
om man vil se på den koden. Bruker man istedet from module1 import function1
og from module2 import function2 så ser man direkte at function1 er
definert i module1 og function2 er definert i module2. Dessuten kan
det hende at et navn på en funksjon i modulen du importerer (som du ikke ens
bruker) klasjer med et navn i din kode.
Oppgave 1¶
Lag et bibliotek uke_11_oppg_1.py i den samme mappen sånn at det følgende
programmet fungerer:
import uke_11_oppg_1
data = [3, 1, 7, -3, 5, 9, 1, 5, 9, 7, -3, 7]
a = uke_11_oppg_1.mean(data)
b = uke_11_oppg_1.median(data)
c = uke_11_oppg_1.mode(data)
print(a, b, c)
Mer spesifikasjon:
Du får ikke bruke de eksisterende funksjonene
mean,medianogmodefra Python.Alle funksjonene skal ta én liste som argument.
Funksjonen
mean(xs)skal returnere gjennomsnittet av tallene i listen. Gjennomsnittet av tallene \(x_1, x_2, ..., x_n\) beregnes med formelen:\[\frac{x_1 + x_2 + ... + x_n}{n}.\]For eksempel:
uke_11_oppg_1.mean([2, 5, 3, 1]) # skal returnere 2.75
Funksjonen
median(xs)skal returnere medianen av tallene i listen. Dette er tallet som er i mitten etter att listen er blitt sortert. Om lengden av listen er jevn er medianen gjennomsnittet av de to tallene i mitten. For eksempel:uke_11_oppg_1.median([4, 12, 3, 9, 5]) # skal returnere 5 uke_11_oppg_1.median([3, 6, 93, 45, 14, 22]) # skal returnere 18
Funksjonen
mode(xs)skal returnere typetallet: det vanligste tallet i listen. Om flere tall er like vanlige skal funksjonen returnere det tallet som står først i listen. For eksempel:uke_11_oppg_1.mode([3, 4, 22, 7, 4, 15, 4, 7, 1]) # skal returnere 4 uke_11_oppg_1.mode([3, 22, 7, 4, 15, 4, 7, 1, 4, 7, 22, 15, 22]) # skal returnere 22
Eksempel 2¶
Når du skriver Pythonkode i en fil, finnes det alltid en (skjult) variabel som
heter __name__ (her er det to understrekk «_» på hver side).
Verdien til __name__ er "__main__" hvis filen kjøres direkte fra
terminalen. F.eks hvis man kjører eksempel_2.py fra terminalen slik:
python eksempel_2.py, så vil variabelen __name__ ha verdien
"__main__".
Hvis eksempel_2.py importeres fra en annen Python fil, det vil si den blir
ikke direkte kjørt fra terminalen, så er variabelen __name__ satt til
"eksempel_2", altså navnet på modulen.
Noen ganger vil vi kjøre noe kode i en fil KUN hvis filen blir kjørt direkte,
men ikke hvis den blir importert av en annen modul / Python fil. For å gjøre
dette skriver vi if name == "__main__":, og putter koden som skal kjøre hvis
vi kjører filen direkte fra terminalen innenfor denne if-clause.
Last ned eksempel_2.py og kjør filen fra terminalen. Skriver funksjonen
hello ut? Hva er verdien på __name__?
# if __name__ == "__main__" example
print('This is the top level, or 0 indentation level, of eksempel_2.py')
def hello():
print('hey there')
if __name__ == "__main__":
print('eksempel_2.py is being run directly')
print(f'{__name__} is the value of __name__') #what prints here?
else:
print('eksempel_2.py is being imported')
print(f'{__name__} is the value of __name__') # what prints here?
hello() # we only call function if file is imported
Nå skal vi se hva __name__ er hvis vi kjører python rett fra terminalen.
Åpne en terminal i samme mappe som filen eksempel_2.py, og skriv python3.
Skriv så
import eksempel_2. Hva skjer nå?Hva er verdien på
__name__?Skriver funksjonen
hellout denne gangen?
Standardbiblioteker¶
Mange nyttige biblioteker er allerede med i hver Python-installasjon, det er «Python Standard Library». Vi skal vise noen eksempler av nyttige moduler her.
En full oversikt finnes på Pythons hovedsiden:
https://docs.python.org/3/library/ Når man kommer til å jobbe mer med Python er
det lurt å bli kjent med oversikten her. Man trenger ikke å være ekspert i alle
modulene, men man må ha en idé hva slags moduler det finnes. Moduler som sys
eller os er brukt i nesten alle prosjektene, mens biblioteker som f.eks
sunau (Read and write Sun AU audio files) har en veldig spesialisert
målgruppe.
Dokumentasjonen for hvert bibliotek er veldig bra, med mange eksempler. Det finnes alltid noe nyttig når man leser gjennom. Du trenger ikke pugge modulene og bibliotekene vi skal diskutere denne uken. Bruk Python dokumentasjonen som en referanse.
Obs
Det kan ta litt tid til å bli vant med å lese dokumentasjon, men det er veldig bra å kunne. Et tips når du vil lese dokumentasjon er å først se på eksemplene og prøve å finne et eksempel som tilsvarer det du vil gjøre. Etter det leser du dokumentasjonen for de tingene som var med i eksemplet/eksemplene.
Eksempel 3¶
Pythons bibliotek math inneholder mange vanlige matematiske funksjoner
og konstanter. Du finner dokumentasjonen for biblioteket på
https://docs.python.org/3/library/math.html.
Her er noen eksempler på bruk av math (du kan laste ned koden her:
eksempel_3.py):
import math
# The floor and ceiling functions
print(f"{4 / 3}")
print(f"{math.floor(4 / 3)}")
print(f"{math.ceil(4 / 3)}")
print()
# The constant e and powers of it
print(f"{math.e}")
print(f"{math.exp(1)}")
print(f"{math.exp(0)}")
print(f"{math.exp(2)}")
print()
# Logarithms
print(f"{math.log(math.e)}")
print(f"{math.log(1)}")
print(f"{math.log(5)}")
print()
print(f"{math.log2(2)}")
print(f"{math.log2(1)}")
print(f"{math.log2(5)}")
print(f"{math.log2(8)}")
print()
print(f"{math.log10(10)}")
print(f"{math.log10(1)}")
print(f"{math.log10(5)}")
print(f"{math.log10(100)}")
print()
# Exponentials
print(f"{math.pow(2, 3)}")
print(f"{math.pow(2, math.log2(3.3))}")
print(f"{math.pow(4, 1 / 2)}")
print(f"{math.sqrt(4)}")
print(f"{math.sqrt(math.pow(3, 4))}")
# print(f"{math.sqrt(-1)}") # This raises an error
# Use the library 'cmath' for complex numbers
print()
from math import pi
print(f"{pi}")
# The trigonometric functions take input in radians, not degrees
# What should all these values be?
print(f"{math.sin(pi / 2)}")
print(f"{math.sin(pi)}")
print(f"{math.cos(pi / 2)}")
print(f"{math.cos(pi)}")
print(f"{math.tan(pi)}")
print(f"{math.tan(pi / 2)}")
Det finnes også andre bibliotek for å gjøre beregninger. Her er en liste på numeriske biblioteker. Se på noen av dem og lag dine egne eksempler.
Eksempel 4¶
Om man trenger en kalender eller må beregne tidspunkt, er det best å bruke en ferdig bibliotek. I Python er det datetime.
Les gjennom siden og se på eksemplene der.
Filen eksempel_4.py viser noen enkle bruk av biblioteken:
from datetime import date
today = date.today()
my_birthday = date(today.year, 6, 24)
if my_birthday < today:
my_birthday = my_birthday.replace(year=today.year + 1)
time_to_birthday = abs(my_birthday - today)
print(time_to_birthday)
from datetime import datetime
now = datetime.now()
exam = datetime(2022, 5, 27, 9, 0, 0)
print(exam - now)
Prøv å legge inn noe du fant i dokumentasjonen.
Oppgave 2¶
Følgende tekst er fra Project Euler nr.19:
«How many Sundays fell on the first of the month during the twentieth century (1 Jan 1901 to 31 Dec 2000)?»
Vi skal svare på dette spørsmålet for fredager som føll på den 2. i måneden.
I filen
uke_11_oppg_2.py skriv kode som bruker datetime-biblioteket til å
beregne og så skrive ut på skjermen hvor mange fredager som føll på den 2.
i maneden fra 1. januar 1901 til 31 desember 2000.
Obs
Her igjen finner du dokumentasjonen for datetime.date
Eksempel 5¶
Når vi vil telle antall kan vi bruke klassen Counter i biblioteket collections,
som er en spesiell versjon av dict(), hvor hvert element begynner med 0 allerede.
Dokumentasjonen finner du her:
collections.
Vi prøver igjen
å telle antall ord i en tekst, men denne gangen bruker vi Counter. Du kan laste
ned koden her: eksempel_5.py.
from collections import Counter
text = """Alice was beginning to get very tired of sitting by her sister
on the bank, and of having nothing to do: once or twice she had peeped
into the book her sister was reading, but it had no pictures
or conversations in it, 'and what is the use
of a book,' thought Alice 'without pictures or conversation?'"""
letter_count = Counter() # instead of dict() or {}
# Count letters
for let in text:
let = let.lower()
if let in "abcdefghijklmnopqrstuvwxyz":
letter_count[let] += 1
# With Counter we don't have to first create a key for every letter
for let, count in letter_count.items():
print(f"{let} is used {count:3d} times")
print("\n\n\n")
word_count = Counter()
for word in text.split():
word = word.lower()
word_count[word] += 1
# With Counter we don't have to first create a key for every word
# The 5 most used words, Counter has a useful helper function most_common()
# we don't need to sort ourselves
print("The 5 most common words")
print(word_count.most_common(10))
for w, c in word_count.most_common(5):
print(f"{w:14} is used {c:3d} times")
Eksempel 6¶
itertools-biblioteken
gjør det enklere å skrive ulike typer løkke. Filen eksempel_6.py viser et tilfelle, men det finnes mange eksempler i dokumentasjonen. Gjerne prøv noen av dem.
import itertools
print("All DNA triples")
bases = "ATGC"
# for i in bases:
# for j in bases:
# for k in bases:
# print(i+j+k)
# the below two lines do the same as the above commented lines
for i, j, k in itertools.product(bases, repeat=3):
print(i + j + k)
Oppgave 3¶
Anta at du underviser i et kurs der hver av studentene dine får tildelt en anonym ID som starter på 1 og går opp til antall studenter som er påmeldt kurset. For eksempel vil ID-ene til et kurs med 20 studenter være:
id_col = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
Du angir om en student har bestått eller ikke bestått emnet med 0 for ikke bestått og 1 for bestått. For et emne med 20 studenter vil denne datakolonnen se slik ut:
pass_fail_col = [0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0]
Du avslutter semesteret og må levere en liste til administrasjonen over hvem som kvalifiserer til å ta eksamen.
I filen uke_11_oppg_3.py, skriv en funksjon som heter select_pass(id_col, pass_fail_col) som ta som input to lister, en av student-IDer og en av studenters bestått/ikke bestått resultater. Funksjonen skal returneres IDer i en liste av bestått studentene. Funksjonen skal fungere med ulike kursstørrelser. Denne oppgaven er lett, men ideen er å søk i dokumentasjonen og bruke en funksjon fra itertools
Eksempelkjøring:
>>> select_pass(id_col,pass_fail_col)
[5, 6, 8, 12, 15]
Eksempel 7a¶
Du kan bruke biblioteket random til å generere tilfeldige tall.
Dokumentasjonen for dette biblioteket finner du her.
Du kan laste ned koden her: eksempel_7a.py. Prøv å kjør koden noen
ganger uten random.seed(123457) og noen ganger med random.seed(123457).
Hva er forskjellen?
import random
# random.seed(123456) # reproduserbare resultater, ulik for hver int
# randint() simulates a random integer
print(f"A random dice throw: {random.randint(1,6)}") # 1 <= N <= 6
print()
foods = ["pancakes", "soup", "stir fry", "lasagne"]
# choice() simulates a random choice among a collection of things
print(f"Today's lunch is: {random.choice(foods)}")
# choices() simulates a list of choices
print(f"This week's lunches are: {random.choices(foods, k=7)}")
print()
people = ["Person A", "Person B", "Person C", "Person D", "Person E"]
# sample() simulates a random sample among a collection of things
print(f"The people selected for the trial are: {random.sample(people, k=3)}")
print()
cards = []
for i in range(1, 14):
cards += [("hearts", i), ("clubs", i), ("spades", i), ("diamonds", i)]
print(f"Unshuffled card deck: {cards[:6]}...")
print()
# shuffle() simulates a random permutation
random.shuffle(cards)
print(f"Shuffled card deck: {cards[:6]}...")
print()
print(f"Player 1 takes the first 3 cards: {cards[:3]}")
print()
# random() without arguments simulates a uniform distribution
# over the interval [0.0, 1.0)
print(f"A random number in the interval [0.0, 1.0): {random.random()}")
print()
# uniform() simulates a uniform distribution over the given interval
print(
f"A random number in the interval [12, 20]: {random.uniform(12.0, 20.0)}"
) # 12.0 <= N <= 20.0
# gauss() simulates a normal distribution with the given
# the mean and standard deviation
mu = 40
sigma = 12
print(
f"A random number from a normal distribution with mean={mu}"
+ f" and standard deviation={sigma}: {random.gauss(mu, sigma)}"
)
Eksempel 7b¶
Vi kan bruke random til å se om vår egen implementasjon av en funksjon som
beregner standardavvikelse fungerer som den skall.
Du kan laste ned koden her: eksempel_7b.py. Prøv å kjør koden noen
ganger med ulike verdier. Ser standard_deviation() ut til å fungere som den
skal?
from random import gauss
from math import sqrt
from statistics import mean
# we define our own standard deviation function
def standard_deviation(data):
data_mean = mean(data)
s = sum([(x - data_mean) ** 2 for x in data])
return sqrt(s / (len(data) - 1))
if __name__ == "__main__":
# we check that it behaves as it should
sigma = 12 # try with different values
data = [gauss(40, sigma) for _ in range(20000)]
print(f"{standard_deviation(data) = }")
print(f"Expected value: {sigma}")
Eksempel 7c¶
Vi kan også bruke random for simulering og analyse. La oss demonstrere dette med Python-turtle og tilfeldige turer
Anta for eksempel at skilpadden tar 100 skritt på en tilfeldig bane fra startposisjonen i midten av lerretet. Skilpadden utfører totalt fem av disse tilfeldige turene.
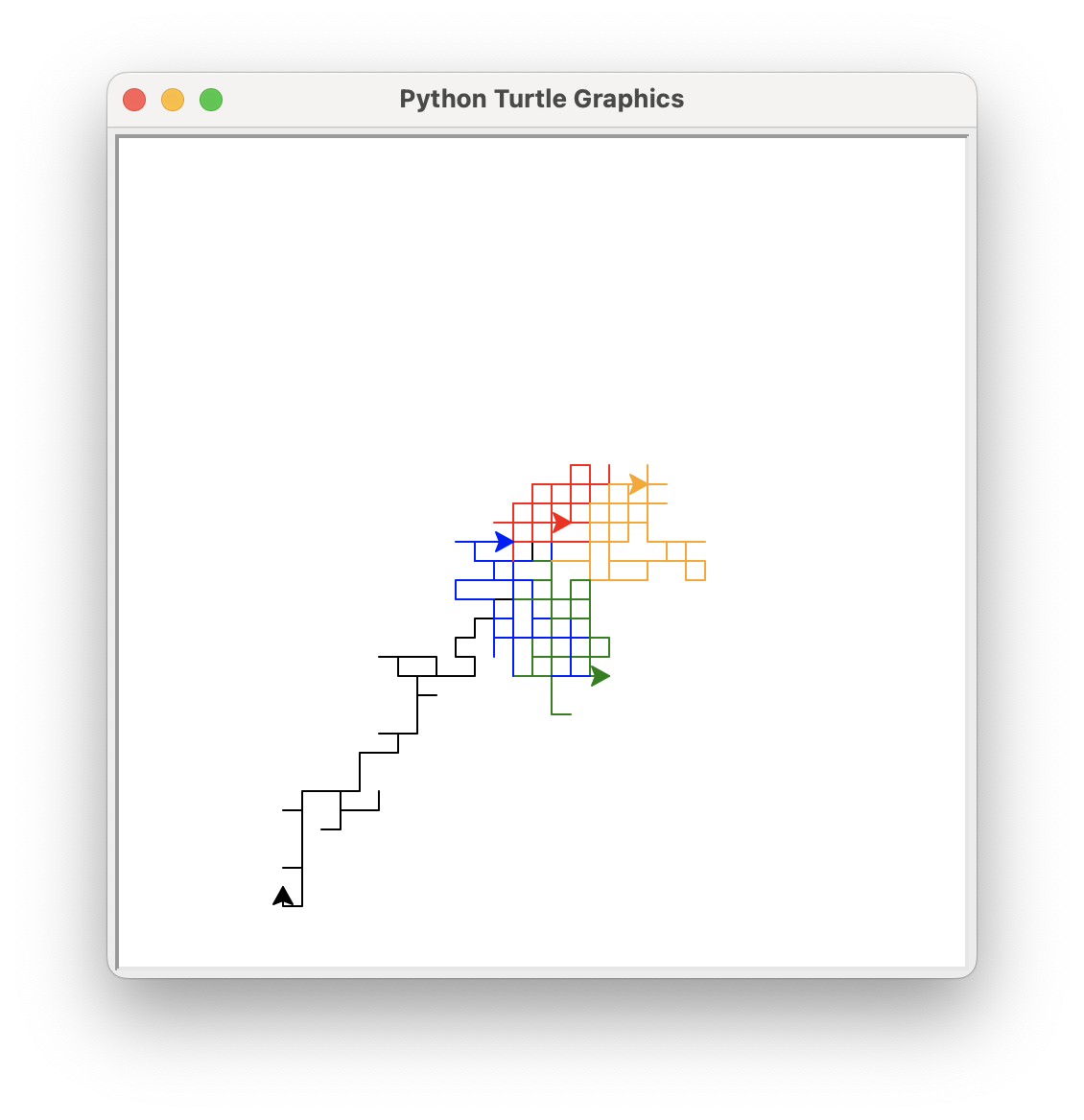
Du kan deretter analysere resultatene av denne serien med tilfeldige turer, for eksempel beregne i gjennomsnitt hvor langt skilpadden har reist fra startposisjonen. Dette resultatet samsvarer med et velkjent matematisk-fenomen - vet du hva det er?
Du kan laste ned koden her: eksempel_7c.py.
import turtle as t
import random
import math
from statistics import mean
t.setup(1000, 1000) # set canvas size
t.hideturtle()
steps = 100
step_size = 10
distances = []
# create 5 turtles
a = t.Turtle()
b = t.Turtle()
c = t.Turtle()
d = t.Turtle()
e = t.Turtle()
# assign different color to each turtle
a.color("red")
b.color("green")
c.color("blue")
d.color("orange")
e.color("black")
turtles = [a, b, c, d, e]
for tu in turtles:
# instructions for walk path
tu.goto(0, 0)
tu.speed(0)
tu.down()
for _ in range(steps):
direction = random.choice([0, 90, 180, 270]) # grid walk
# direction = random.uniform(0,360) # any direction allowed
tu.setheading(direction)
tu.forward(step_size)
tu.up()
# distance traveled is the square root of the sum of squared change in x and squared change in y
xdist = tu.xcor()
ydist = tu.ycor()
d = math.sqrt(xdist**2 + ydist**2)
distances.append(d)
print(distances)
print(f"Direct way to calculate average distance yields {mean(distances):.2f}")
# check against theory (holds true for many repetitions of random walk, fewer repetitions is less accurate)
avg_distance = step_size * math.sqrt(steps)
print(f"Theoretical calc for avg distance is {avg_distance:.2f}")
t.done()
Oppgave 4¶
Vi skal regne ut verdien til \(\pi\) ved å simulere mange tilfeldige (x, y) punkter mellom 0 og 1. Så teller vi opp hvor mange av punktene ligger inni kvartsirkelen med radius 1 sammenlignet med antallet punkter i alt:
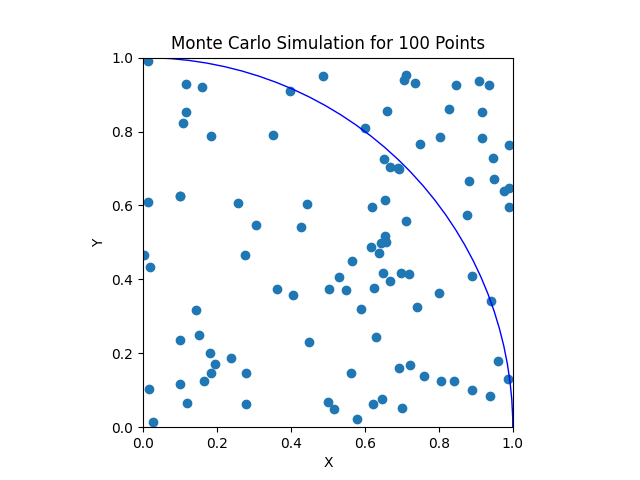
Denne andelen tilsvarer forholdet mellom arealene til kvartsirkelen og firkantet:
I vårt eksempel fra 0 til 1 er areal til kvartsirkelen \(\frac{1}{4}\pi\) og arealen til kvadratet er 1.
eller, med \(\pi\) på venstre siden,
Jo flere punkter vi simulerer, jo presisere blir verdien til \(\pi\):
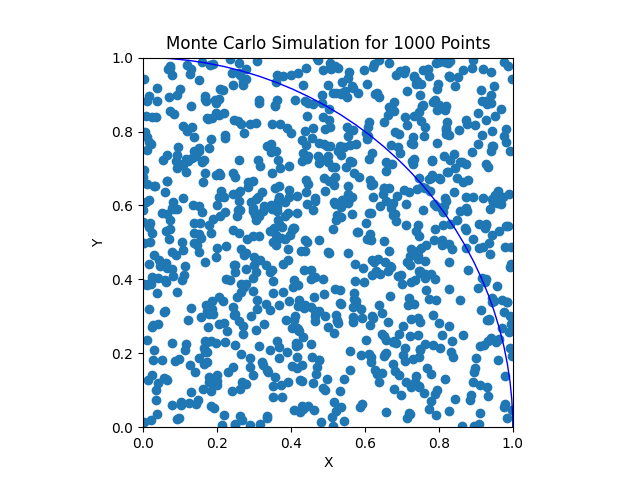
I filen uke_11_oppg_4.py, skriv en funksjon med navn find_pi(N) som tar som argument antallet punkter N som skal simuleres. Bruk så random-biblioteket for å lage N x- og y-verdier. En punkt ligger inni sirkelen når x**2 + y**2 <= 1. Funksjonen skal returnere antallet punkter inni sirkelen dividert med antallet i alt, dvs. N.
Prøv funksjonen din med N = 1000 og N = 10000 punkter også. Når N blir større, kommer da verdien som du beregner nærmere til \(\pi\) ?
Eksempel 8¶
Biblioteken fractions og decimal kan brukes til beregninger om man vil undvike avrundingsfeil som man får om man bruker float.
For å lage en desimal skriver du for eksempel Decimal("0.2"). For å lage en
brøkdel skriver du for eksempel Fraction(10, 5). Det første argumentet er
teller og det andre argumentet er nevner. Fraction kan gjøre forenklinger
akkurat som vi gjør på papir når vi regner med brøkdeler. Vi kan også bruke
Fraction til å finne den nermeste ratsjonelle approsimasjonen av et
irratsjonellt tall med en øvre grens på nevneren.
from decimal import Decimal
from fractions import Fraction
from math import pi
# using Decimal avoids rounding errors
print(f"Using floats: {0.1 + 0.2 = }")
print(f"Using Decimal: 0.1 + 0.2 = {Decimal('0.1') + Decimal('0.2')}")
print()
print(f"Using floats: {(1/14) * (7/3) = }")
print(f"Using Fraction: (1/14) * (7/3) = {Fraction(1, 14) * Fraction(7, 3)}")
print()
# we can use the fractions library to find the closest fraction to a given number
print(
"The closest fraction to π with denominator at most 1000 is:",
str(Fraction(pi).limit_denominator(1000)),
)
Oppgave 5¶
I denne oppgaven skal du bruke biblioteket decimals til å skrive et program som produserer en kvittering fra en butikk.
Last ned uke_11_oppg_5.py og spar den på datamaskinen din (med samme
navn). Filen ser slik ut:
def receipt_content(prices_filename, cash_register_filename):
"""Construct contents of a receipt of the cash register events,
given the store prices."""
# din kode her
def receipt(prices_filename, cash_register_filename):
"""Construct a receipt of the cash register events,
given the store prices."""
# get receipt content from receipt_content()
purcases_returns, total, vat, payment, change = receipt_content(
prices_filename, cash_register_filename
)
# the formatted lines of the receipt
receipt_lines = [f"{'Nr.':>4} {'Item':18} {'Price':>10}"]
for nr, item, price in purcases_returns:
receipt_lines.append(f"{nr:4d} {item:18} {price:10.2f}")
receipt_lines.append(f"Total: {total}")
receipt_lines.append(f"Of which VAT: {vat:.2f}")
receipt_lines.append(f"Payment: {payment}")
receipt_lines.append(f"Change {change}")
# add some dividers
max_len = max(len(line) for line in receipt_lines)
divider = "-" * max_len
receipt_lines.insert(1, divider)
receipt_lines.insert(-4, divider)
receipt_lines.insert(-2, divider)
return "\n".join(receipt_lines)
Du skal skrive koden til funksjonen receipt_content() som beregner
inneholdet i kvitteringen utifra en fil med butikkens priser og en fil med
hendelsene ved kassen. Argumentet prices_filename er en streng med navnet
til filen som inneholder prisene. Argumentet cash_register_filename er en
streng med navnet til filen som inneholder hendelsene ved kassen.
Funksjonen receipt_content() skal returnere en tupel som inneholder følgende
(i denne orden):
En liste med tupler som inneholder (i følgende orden) antall, produkt og totalt pris, først for alle ting som har blitt kjøpt, i alfabetisk orden, og så for alle ting som har blitt returnert, i alfabetisk orden (se eksempelkvittering nedenfor). For de returnerte produktene blir det negative tall.
Det totale priset.
Hvor mye av det totale priset som er mva.
Hvor mye som har blitt betalt.
Hvor mye som blir betalt tilbake (her blir det ikke-positive tall).
Filen med butikkens priser er formattert slik som eksempelfilen
prices.txt (som du kan bruke til å teste programmet ditt):
banana;7.40
dish soap;26.20
toilet paper;34.00
apple;5.00
frozen pizza;54.40
stamp;3.00
bread;22.20
ice cream;35.10
toothpaste;13.70
pocket book;149.00
chips;24.30
tomato;10.00
peanuts;18.50
Først står produkt, så «;», og så priset.
Filen med hendelsene ved kassen er formattert slik som eksempelfilen
cash_register.txt (som du kan bruke til å teste programmet ditt):
buy;apple
buy;dish soap
buy;apple
buy;toilet paper
buy;frozen pizza
buy;peanuts
return;toothpaste
buy;tomato
buy;chips
buy;tomato
return;pocket book
buy;tomato
pay;100.00
Først står hva som skjer (kjøp, retur eller betaling), så «;», og så produkten/verdien.
Funksjonen receipt() skal du ikke endre. Den bruker receipt_content()
til å beregne inneholdet i kvitteringen og så produserer receipt() en pen
kvittering utifra det innholdet. Du skal bare skrive kode til
receipt_content(). Om din kode til receipt_content() er riktig så skal
du for eksempel få følgende streng når du bruker receipt("prices.txt",
"cash_register.txt"):
Nr. Item Price
------------------------------------
2 apple 10.00
1 chips 24.30
1 dish soap 26.20
1 frozen pizza 54.40
1 peanuts 18.50
1 toilet paper 34.00
3 tomato 30.00
-1 pocket book -149.00
-1 toothpaste -13.70
------------------------------------
Total: 34.70
Of which VAT: 6.94
------------------------------------
Payment: 100.00
Change -65.30
Din kode skal inneholde to egendefinerte exceptions:
Om priset til en produkt som kjøpes/returneres ikke finnes i prislisten skal koden produsere (
raise) en egendefinert Exception som heterNoPrice(uten melding). (Denne skal ikke fanges av programmet uten programmet skal krasje med denne feiltypen.)Om kunden har ikke betalt nok skal koden produsere (
raise) en egendefinert Exception som heterNotEnoughPaid(uten melding). (Denne skal ikke fanges av programmet uten programmet skal krasje med denne feiltypen.)
Mer spesifikasjon og tips:
Du må bruke biblioteket decimals for at beregningene skal bli riktige (prøv hvordan kvitteringen blir om du bruker
float).Det er mulig at betaling skjer flere ganger underveis ved kassen.
Du kan anta at alle betalinger ved kassen har positiv verdi.
Du kan anta at det ikke er noen feil i filene som inneholder prisene og hendelsene ved kassen.
Det er mulig at det totale priset blir negativt (om kunden for eksempel bare returnerer ting).
Gitt et pris inklusive mva så multipliserer du priset med \(0.2\) for å finne ut hvor mye av priset som er mva.
Det kan være lurt å bruke dictionaries til prislisten og det som blitt kjøpt og det som blitt returnert.
Du må ikke skrive all kode innen funksjonen
receipt_content(). Du kan dele opp koden i flere funksjoner på en måte du synes føles naturlig.
Oppgaver¶
Obs
Testene tilgjengelig her: uke_11_tests.zip for oppgavene 1, 3 og 4.
Oppgave 1¶
Du finner Oppgave 1 nedenfor Eksempel 1.
Oppgave 2¶
Du finner Oppgave 2 nedenfor Eksempel 4.
Oppgave 3¶
Du finner Oppgave 3 nedenfor Eksempel 6.
Oppgave 4¶
Du finner Oppgave 4 nedenfor Eksempel 7.
Oppgave 5¶
Du finner Oppgave 5 nedenfor Eksempel 8.